Funkcja skokowa Heaviside’a

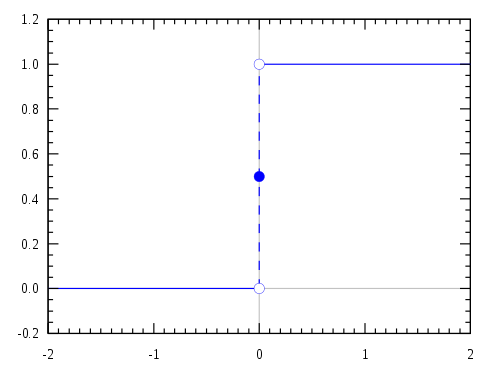
Funkcja skokowa Heaviside’a, skok jednostkowy – funkcja nieciągła, która przyjmuje wartość ${\displaystyle 0}$ dla ujemnych argumentów i wartość ${\displaystyle 1}$ w pozostałych przypadkach:

${\displaystyle H(x)={\begin{cases}0\ \mathrm {dla} \ x<0\\1\ \mathrm {dla} \ x\geqslant 0\end{cases}}.}$

Często stosowanym symbolem, zwłaszcza w środowisku inżynierskim elektryków i elektroników, dla funkcji skokowej Heaviside’a jest ${\displaystyle \mathbf {1} {\big (}t{\big )}}$ (np. ^[1], symbolu tego używał sam Oliver Heaviside^[2]). Argument ${\displaystyle t}$ oznacza tu zazwyczaj czas. Przy zastosowaniach z dziedziny mechaniki, na przykład analizie belek, argumentem tej funkcji może być położenie obciążenia.

Funkcja ta jest używana w przetwarzaniu sygnałów do reprezentowania sygnału włączającego się w danej chwili czasu, w elektrotechnice i elektronice do analizy stanów nieustalonych w obwodach RLC, w automatyce jako sygnał wymuszenia na wejściu układu, a także w mechanice do reprezentowania obciążeń belek rozłożonych na pewnej części ich długości.

Skok jednostkowy jest wynikiem całkowania delty Diraca^[3]. Wartość funkcji Heaviside’a dla argumentu 0 nie jest szczególnie istotna, ponieważ funkcja jest zazwyczaj używana wewnątrz całki. Niektóre źródła podają ${\displaystyle H(0)=0,}$ a inne ${\displaystyle H(0)=1.}$ Używa się też wartości ${\displaystyle H(0)=0{,}5,}$ aby uzyskać symetrię funkcji. Definicja ${\displaystyle H(x)}$ wygląda wtedy następująco^[4]:

${\displaystyle \int \limits _{-\infty }^{x}{\delta (t)dt}=H(x)=={\begin{cases}0\ \quad \quad {\text{dla }}\,t<0\\{\frac {1}{2}}\quad \quad {\text{dla }}\,t=0\\1\quad \quad \,{\text{dla }}\,t>0\end{cases}}}$

Funkcja skoku jednostkowego spełnia ważną rolę w rachunku operatorowym, m.in. przekształcenie Laplace’a zawiera ją w sposób niejawny.

• charakterystyka skokowa
• funkcja signum
• transmitancja operatorowa