Obwiednia

Ten artykuł dotyczy matematyki. Zobacz też: obwiednia sygnału (ogólnie), obwiednia dźwięku (syntezatory).

Obwiednia (ang. envelope) – matematyczne pojęcie z zakresu geometrii różniczkowej. Obwiednia rodziny rozmaitości różniczkowych (w szczególności rodziny krzywych lub powierzchni) jest rozmaitością w każdym swoim punkcie styczną do pewnego członka tej rodziny^[1]. W otoczeniu dowolnego punktu należącego do obwiedni znajdują się zatem zarówno punkty należące do członków tej rodziny, jak i punkty nienależące do żadnego z członków.

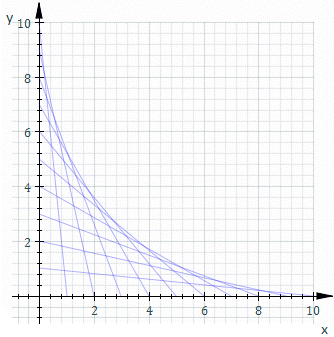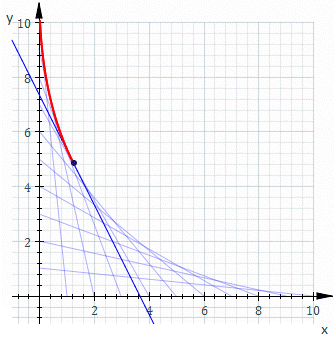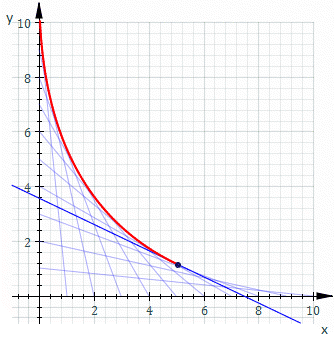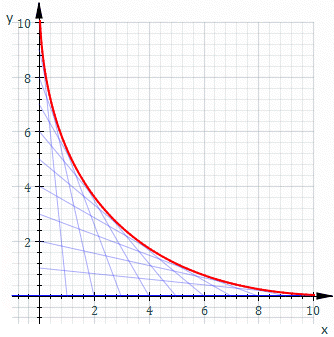
Niech dane będzie odwzorowanie p opisujące ${\displaystyle (n-1)}$-wymiarową powierzchnię zanurzoną w ${\displaystyle n}$-wymiarowej przestrzeni w czasie ${\displaystyle t{:}}$

${\displaystyle \mathbb {R} ^{n-1}\times \mathbb {R} \supset U\ni (\mathbf {u} ,t)\mapsto \mathbf {p} (\mathbf {u} ,t)\in \mathbb {R} ^{n}}$

Obwiednią E powierzchni p względem parametru ${\displaystyle t}$ jest zbiór punktów spełniających warunek:

${\displaystyle {\frac {\partial \mathbf {p} }{\partial t}}(\mathbf {u} ,t)\in T_{\mathbf {p} (\mathbf {u} ,t)}}$

gdzie ${\displaystyle T_{\mathbf {p} (\mathbf {u} ,t)}}$ jest liniową podprzestrzenią styczną do powierzchni ${\displaystyle \mathbf {p} }$ w punkcie ${\displaystyle \mathbf {p} (\mathbf {u} ,t=\mathrm {const} ).}$ Przestrzeń styczna jest rozpięta na wektorach ${\displaystyle {\frac {\partial \mathbf {p} }{\partial u^{i}}}}$ (dla ${\displaystyle i=0,\dots ,n-1}$). Opisany warunek można zapisać:

${\displaystyle \det \left=0}$

Dla przypadku trójwymiarowego (n=3) równanie obwiedni powierzchni ${\displaystyle \mathbf {p} (u,v,t)\in \mathbb {R} ^{3}}$ ma postać:

${\displaystyle \det \left=0}$

Powyższe równanie może być zapisane z użyciem iloczynu skalarnego wektora ${\displaystyle {\tfrac {\partial \mathbf {p} }{\partial t}}}$ oraz wektora normalnego ${\displaystyle n}$ do powierzchni p w punkcie ${\displaystyle (u,v){:}}$

${\displaystyle \left\langle {\tfrac {\partial \mathbf {p} }{\partial t}},\mathbf {n} (u,v)\right\rangle =0}$

gdzie ${\displaystyle n(u,v)}$ jest iloczynem wektorowym pochodnych cząstkowych odwzorowania p:

${\displaystyle \mathbf {n} (u,v)={\frac {\partial \mathbf {p} }{\partial u}}\times {\frac {\partial \mathbf {p} }{\partial v}}}$

Jednostkowy okrąg poruszający się ruchem prostoliniowym wzdłuż osi OX w przestrzeni dwuwymiarowej OXY jest sparametryzowany kątem ${\displaystyle \alpha {:}}$

${\displaystyle \mathbf {p} (\alpha ,t)=(\cos \alpha +t,\sin \alpha )}$

pochodne cząstkowe względem ${\displaystyle \alpha }$ i ${\displaystyle t}$ wynoszą:

${\displaystyle {\frac {\partial \mathbf {p} }{\partial \alpha }}=(-\sin \alpha ,\cos \alpha )}$

${\displaystyle {\frac {\partial \mathbf {p} }{\partial t}}=(1,0)}$

Równanie obwiedni ma zatem postać:

${\displaystyle \det \left=0\Leftrightarrow \cos \alpha =0\Leftrightarrow \alpha ={\frac {\pi }{2}}+n\pi }$

zaś samą obwiednię stanowią dwie proste ${\displaystyle y=1}$ oraz ${\displaystyle y=-1}$ na płaszczyźnie OXY.

Niech dana będzie powierzchnia w przestrzeni ${\displaystyle n}$-wymiarowej opisana równaniem:

${\displaystyle F(\mathbf {p} ,t)=0}$

gdzie ${\displaystyle \mathbf {p} \in \mathbb {R} ^{n},}$ ${\displaystyle t\in \mathbb {R} }$ oraz ${\displaystyle F:\mathbb {R} ^{n}\times \mathbb {R} \mapsto \mathbb {R} .}$ Obwiednią E powierzchni opisanej przy pomocy ${\displaystyle F}$ są punkty ${\displaystyle (\mathbf {p} ,t),}$ dla których spełnione są:

${\displaystyle {\frac {\partial F}{\partial t}}(\mathbf {p} ,t)=0\wedge F(\mathbf {p} ,t)=0}$

Jednostkowy okrąg poruszający się ruchem prostoliniowym wzdłuż osi OX w przestrzeni dwuwymiarowej OXY opisany jest za pomocą:

${\displaystyle F(x,y,t)=(x-t)^{2}+y^{2}-1=0}$

Pochodna cząstkowa ${\displaystyle F}$ względem ${\displaystyle t}$ wynosi:

${\displaystyle {\frac {\partial F}{\partial t}}=-2(x-t)}$

Równanie obwiedni ma zatem postać:

${\displaystyle \left\{{\begin{array}{l}F(x,y,t)=(x-t)^{2}+y^{2}-1=0\\{\frac {\partial F}{\partial t}}(x,y,t)=-2(x-t)=0\end{array}}\right.}$

z czego wynika, iż samą obwiednię stanowią dwie proste ${\displaystyle (x=t,y=\pm 1).}$

• geometria różniczkowa
• krzywa
• powierzchnia

• Flaquer J., Garate G., Pargada M.: Envelopes of moving quadric surfaces, CAGD 9, 1992.
• Eisenhart L.P.: A Treatise on the Differential Geometry of Curves and Surfaces, Dover 2004.

• Eric W.E.W. Weisstein Eric W.E.W., Envelope, MathWorld, Wolfram Research   (ang.).