Funkcja osobliwa
Dzisiaj Funkcja osobliwa jest tematem o dużym znaczeniu i zainteresowaniu w dzisiejszym społeczeństwie. Coraz więcej osób angażuje się i interesuje Funkcja osobliwa, szukając informacji, opinii i porad na ten temat. W tym artykule szczegółowo zbadamy temat Funkcja osobliwa, analizując jego różne aspekty i oferując kompleksowe podejście, które pozwala czytelnikom lepiej zrozumieć jego znaczenie i implikacje. Od powstania do dzisiejszego wpływu, Funkcja osobliwa to temat, który nie pozostawia nikogo obojętnym, a dzięki temu artykułowi mamy nadzieję przedstawić szeroką i szczegółową wizję, która pomoże wzbogacić wiedzę i zrozumienie tego tematu.
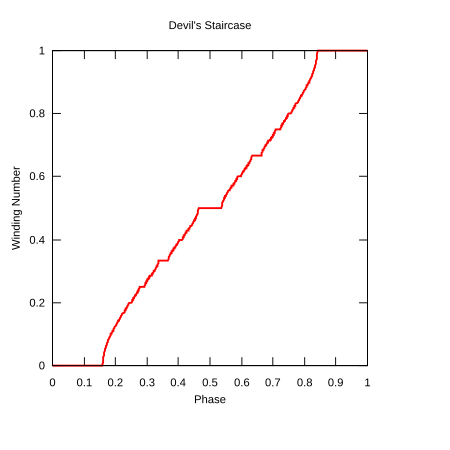
Funkcja osobliwa (określana również jako Diabelskie schody[potrzebny przypis]) – dowolna funkcja ƒ(x), określona dla przedziału , posiadająca następujące właściwości:
- ƒ(x) jest ciągła na .
- istnieje taki zbiór N o mierze 0, że dla każdego x spoza N pochodna ƒ ′(x) istnieje i jest równa zeru, tzn. pochodna f zanika niemal wszędzie. (czyli jest prawie wszędzie różniczkowalna i jej pochodna jest równa 0)
- ƒ(x) nie maleje na .
- ƒ(a) < ƒ(b).
Klasycznym przykładem funkcji osobliwej jest funkcja Cantora, nazywana czasami diabelskimi schodami. Istnieją jednak również inne funkcje tak nazywane. Jedna z nich jest określona przez odwzorowanie koliste.
Jeśli ƒ(x) = 0 dla wszystkich x ≤ a oraz ƒ(x) = 1 dla wszystkich x ≥ b, to można założyć, że dana funkcja przedstawia dystrybuantę dla zmiennej losowej, która ani nie jest cząstkową zmienną losową (gdyż prawdopodobieństwo wynosi zero w każdym punkcie) ani absolutnie ciągłą zmienną losową (gdyż gęstość prawdopodobieństwa jest zerowa wszędzie, gdzie jest określona).
Funkcje osobliwe występują przykładowo w strukturach w roztworach i magnesach, opisywanych przez model Frenkela i Kontorowa oraz model ANNNI, jak również w niektórych układach dynamicznych. Być może najpowszechniejszym przykładem są funkcje leżące u podstaw fraktalnego kwantowego efektu Halla.
Zobacz też
Linki zewnętrzne
- Eric W. Weisstein, Devil's Staircase, MathWorld, Wolfram Research (ang.).
| pojęcia definiujące |
| ||||||||
|---|---|---|---|---|---|---|---|---|---|
| odmiany – warunki wystarczające |
| ||||||||
| uogólnienia – warunki konieczne | |||||||||
| twierdzenia o funkcjach ciągłych |
| ||||||||
| powiązane funkcje |
| ||||||||
| pokrewne tematy | |||||||||
| uczeni według daty narodzin |
|
