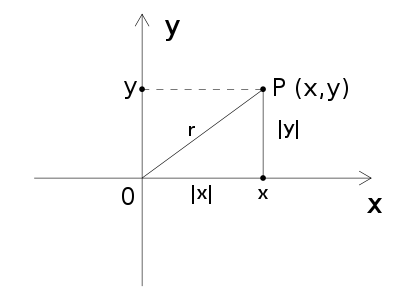Jedynka trygonometryczna

Jedynka trygonometryczna – tożsamość trygonometryczna postaci^[1]:

${\displaystyle \sin ^{2}x+\cos ^{2}x=1.}$

Jest ona prawdziwa dla każdej wartości kąta ${\displaystyle x\in \mathbb {R} ,}$ a także ogólniej dla argumentów zespolonych.

Istnieją również dwie inne wariacje tego wzoru:

${\displaystyle \sec ^{2}x-\operatorname {tg} ^{2}x=1,}$

${\displaystyle \operatorname {cosec} ^{2}x-\operatorname {ctg} ^{2}x=1.}$

Sposób 1:

Niech ${\displaystyle P=(x_{0},y_{0}),\,O=(0,0),\,X_{0}=(x_{0},0),\,\angle {POX_{0}}=\alpha ,\,|OP|=r.}$

Zauważmy, że:

${\displaystyle |\angle {PX_{0}O}|={\frac {\pi }{2}},}$

więc trójkąt ${\displaystyle POX_{0}}$ jest trójkątem prostokątnym o przeciwprostokątnej ${\displaystyle r.}$

Zatem na mocy twierdzenia Pitagorasa:

${\displaystyle r^{2}=|x_{0}|^{2}+|y_{0}|^{2},}$

${\displaystyle r^{2}=x_{0}^{2}+y_{0}^{2},}$

${\displaystyle 1=\left({\frac {x_{0}}{r}}\right)^{2}+\left({\frac {y_{0}}{r}}\right)^{2}.}$

Z definicji funkcji trygonometrycznych wyrażenie

${\displaystyle \left({\frac {x_{0}}{r}}\right)^{2}+\left({\frac {y_{0}}{r}}\right)^{2}}$

jest równe

${\displaystyle \sin ^{2}\alpha +\cos ^{2}\alpha .}$

Zatem

${\displaystyle \sin ^{2}\alpha +\cos ^{2}\alpha =1,}$

q.e.d.

Zauważmy, że to rozumowanie można przeprowadzić również w drugą stronę, co oznacza, że wzór jedynkowy jest równoważny twierdzeniu Pitagorasa. Stąd jedna z jego nazw: postać trygonometryczna twierdzenia Pitagorasa.

Sposób 2:

Ze wzoru Eulera:

${\displaystyle \sin {x}={\frac {e^{ix}-e^{-ix}}{2i}}}$

oraz

${\displaystyle \cos {x}={\frac {e^{ix}+e^{-ix}}{2}}.}$

Zatem

${\displaystyle {\begin{aligned}\sin ^{2}{x}+\cos ^{2}{x}&=\left({\frac {e^{ix}-e^{-ix}}{2i}}\right)^{2}+\left({\frac {e^{ix}+e^{-ix}}{2}}\right)^{2}\\&={\frac {e^{2ix}-2+e^{-2ix}}{-4}}+{\frac {e^{2ix}+2+e^{-2ix}}{4}}\\&={\frac {2+2}{4}}=1,\end{aligned}}}$

q.e.d.

Stąd wynika, że jedynka trygonometryczna jest słuszna w dziedzinie liczb zespolonych.

Sposób 3:

Niech:

${\displaystyle f(x)=\sin ^{2}x+\cos ^{2}x.}$

Zauważmy, że:

${\displaystyle f(0)=\sin ^{2}0+\cos ^{2}0=0^{2}+1^{2}=1.}$

Także:

${\displaystyle f'(x)=(\sin ^{2}x+\cos ^{2}x)'=\sin x\cos x+\sin x\cos x-\sin x\cos x-\sin x\cos x=0.}$

Skoro pochodna funkcji ${\displaystyle f(x)}$ jest równa 0, to funkcja ${\displaystyle f(x)}$ musi być funkcją stałą.

Wiedząc, że ${\displaystyle f(0)=1,}$ oraz że funkcja ${\displaystyle f(x)}$ jest funkcją stałą, możemy dojść do wniosku, że

${\displaystyle \sin ^{2}x+\cos ^{2}x=1.}$

q.e.d.

• funkcje trygonometryczne
• jedynka hiperboliczna