Pięciokąt

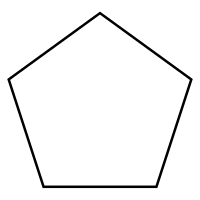
Pięciokąt (pięciobok) – wielokąt o pięciu bokach. Każdy pięciokąt ma pięć przekątnych. Szczególnym przypadkiem pięciokąta jest pięciokąt foremny.

Pięciokąt foremny, pentagon^[1] – wielokąt foremny o pięciu bokach. Pięciokąty foremne są ścianami takich wielościanów jak m.in. dwunastościan foremny i dwudziestościan ścięty.

Pięciokąt foremny o boku długości ${\displaystyle a}$ ma następujące własności:

• każdy jego kąt wewnętrzny ma miarę

${\displaystyle {\frac {3}{5}}\pi =108^{\circ }}$

• kąt środkowy okręgu opisanego oparty na boku pięciokąta ma miarę

${\displaystyle {\frac {2}{5}}\pi =72^{\circ }}$

• pole powierzchni wyraża się wzorem

${\displaystyle P={\frac {5a^{2}}{4}}\operatorname {ctg} {\frac {\pi }{5}}={\frac {a^{2}}{4}}{\sqrt {25+10{\sqrt {5}}}}\approx 1{,}72048\cdot a^{2}}$

• promień okręgu opisanego na pięciokącie foremnym ma długość

${\displaystyle R=a{\frac {\sqrt {50+10{\sqrt {5}}}}{10}}=a{\frac {1}{\sqrt {3-\varphi }}}}$

• promień okręgu wpisanego w pięciokąt foremny ma długość

${\displaystyle r={\frac {a{\sqrt {25+10{\sqrt {5}}}}}{10}}={\frac {\varphi R}{2}}}$

• przekątna ma długość

${\displaystyle d={\frac {{\sqrt {5}}+1}{2}}a=\varphi a,}$

gdzie ${\displaystyle \varphi }$ oznacza złotą liczbę

• wysokość ma długość

${\displaystyle h=a{\frac {\sqrt {5+2{\sqrt {5}}}}{2}}}$

Możliwość skonstruowania przy użyciu cyrkla i linijki pięciokąta foremnego wynika z twierdzenia Gaussa-Wantzela (liczba 5 jest liczbą pierwszą Fermata). Poniżej przedstawiono cztery przykładowe algorytmy; opierają się głównie na własności, że bok pięciokąta foremnego jest złotą częścią jego przekątnej.

Poniższą konstrukcję przedstawił H. W. Richmond w 1893 roku^[2].

1. Narysuj okrąg o środku S.
2. Narysuj średnicę AB.
3. Narysuj promień CS prostopadły do średnicy AB.
4. Znajdź środek D odcinka CS i narysuj odcinek AD.
5. Narysuj dwusieczną kąta ∠ADS, punkt jej przecięcia ze średnicą AB oznacz E.
6. Narysuj prostą prostopadłą do AB przechodzącą przez E, punkt jej przecięcia z okręgiem oznacz F.
7. Odcinek AF jest bokiem pięciokąta wpisanego w wyjściowy okrąg.

Ptolemeusz w swoim dziele Almagest^[3][4] opisuje sposób znalezienia długości boku pięciokąta wpisanego w zadany okrąg.

1. Narysuj okrąg o środku S.
2. Narysuj średnicę okręgu i prostopadły do niej promień BS.
3. Znajdź środek A jednego z promieni zawierających się w średnicy.
4. Narysuj łuk o środku A i promieniu AB, punkt jego przecięcia ze średnicą oznacz C.
5. Odcinek BC ma długość boku pięciokąta wpisanego w wyjściowy okrąg.

Metodę Ptolemeusza można rozbudować, uzyskując algorytm znalezienia wszystkich pięciu wierzchołków na okręgu.

1. Narysuj okrąg o środku S.
2. Narysuj prostą przechodzącą przez S i przecinającą okrąg w punktach A i B.
3. Narysuj promień CS prostopadły do średnicy AB.
4. Znajdź środek odcinka BS i oznacz go D.
5. Narysuj łuk o środku D i promieniu CD, punkty jego przecięcia z prostą AB oznacz E i F.
6. Narysuj łuk o środku C i promieniu CE, punkty jego przecięcia z okręgiem oznacz G i H.
7. Narysuj łuk o środku C i promieniu CF, punkty jego przecięcia z okręgiem oznacz I i J.
8. Punkty C, G, H, I, J są wierzchołkami pięciokąta foremnego.

W poniższej konstrukcji wykorzystano okrąg Carlyle’a^[3].

1. Narysuj okrąg o środku O.
2. Przez punkt O poprowadź prostą k, punkty jej przecięcia z okręgiem oznacz Q i P.
3. Narysuj promień OA prostopadły do średnicy QP.
4. Znajdź środek M promienia OQ.
5. Narysuj okrąg o środku M przechodzący przez A; punkty jego przecięcia z prostą k oznacz V i W.
6. Zakreśl łuk o środku W i promieniu OP, punkty jego przecięcia z wyjściowym okręgiem oznacz P₁ i P₄.
7. Zakreśl łuk o środku V i promieniu OP, punkty jego przecięcia z wyjściowym okręgiem oznacz P₂ i P₃.
8. Punkty P, P₁, P₂, P₃, P₄ są wierzchołkami pięciokąta foremnego.

Zobacz hasło pięciokąt w Wikisłowniku

• kopuła geodezyjna
• kwadrat
• pentagram
• sześciokąt foremny
• trójkąt równoboczny
• złoty podział

• Krzysztof R.K.R. Apt Krzysztof R.K.R., Elegancka konstrukcja pięciokąta foremnego, „Delta”, październik 2024, ISSN 0137-3005  .